Na rozgrzewkę:
W kolejnym wpisie dotyczącym szybkiej transformaty Fouriera przedstawię program służący do obliczenia FFT oraz wyniki na podstawie sygnału z generatora funkcyjnego. Następnie zaprezentuję jak częstotliwość próbkowania oraz okna, wpływają na wyciek widma.
Jeśli chcesz nabyć płytki deweloperskie lub mikrokontrolery STM, na których będziesz mógł wykonać projekty związane z przetwarzaniem sygnałów, zapraszam do sklepu msalamon.pl
Sponsorem wpisu jest msalamon.pl
WWW: https://msalamon.pl/
Sklep: https://sklep.msalamon.pl/
Zakres wpisu:
- Program obliczający FFT
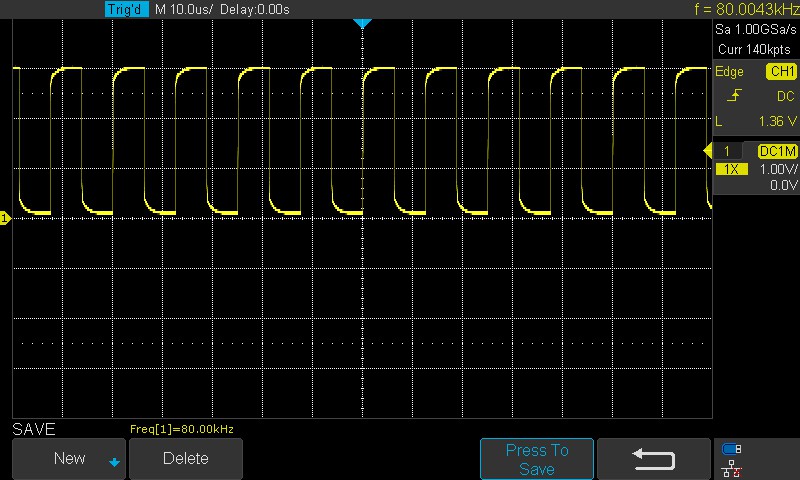
- Sygnał z timera 2 informujący o częstotliwości próbkowania
- Wyniki FFT
- Wyciek widma spowodowany złym doborem częstotliwości próbkowania
- Wyciek widma spowodowany użyciem okien innych niż prostokątne, kiedy sygnał jest okresowy
Program obliczający FFT:
Funkcje uruchamiające używane peryferia: timer 2 wyzwalający konwersję oraz DMA przetwornika analogowo-cyfrowego:
HAL_ADC_Start_DMA(&hadc1, (uint32_t*)&ADC_Buffer, BUFFER_SIZE); HAL_TIM_Base_Start(&htim2); HAL_TIM_PWM_Start(&htim2, TIM_CHANNEL_3);
Inicjalizacja FFT:
arm_rfft_fast_instance_f32 fft_handler; arm_rfft_fast_init_f32(&fft_handler, fftSize);
Funkcja obliczająca FFT:
Bufor wejściowy do FFT składa się z 255 próbek, od wartości maksymalnej. Jest to wycięty przebieg wejściowy oknem prostokątnym.
Napięcie referencji na Discovery wynosi 3.0V, więc wprowadzona składowa stała 1.4V na generatorze będzie wynosiła w LSB 1911, która jest odejmowana w linii 19. Bez usunięcia offsetu największym prążkiem będzie 0, czyli składowa stała.
W poniższym kodzie używane jest okno prostokątne, dlatego za komentowane są linie od 22 do 32. Jeśli chcesz użyć innego okna niż prostokątne, należy od komentować wybrane okno, a za komentować część dotyczącą okna prostokątnego.
void FFT_Calc()
{
if(Buffer_FFT_Status==1)
{
First_calculation_loop=0;
/*Szukanie pierwszego maksimum przy którym naładowane będą kondensatory filtrujące*/
for(uint16_t i=150; i<200; i++)
{
if(ADC_Buffer[i]>Max_value)
{
Max_value_index=i;
Max_value=ADC_Buffer[i];
}
}
/*Bufor zawierający 256 próbkek od wartości maksymalnej stworzony do prezentacji przebiegu wchodzącego do FFT*/
for(uint16_t i=0; i<FFT_SAMPLES; i++)
{
Input_Buffer[i]= ((float32_t) (ADC_Buffer[Max_value_index+i]))-1911.0;
}
/*for(uint16_t i=0; i<FFT_SAMPLES; i++)
{
//Blackman-Harris window
//Input_Buffer_Window[i]=(0.35875 - 0.48829 * cosf((2.0*PI*i) / (FFT_SAMPLES)) + 0.14128 * cosf((4.0*PI*i) / (FFT_SAMPLES)) - 0.01168 * cosf((6.0*PI*i) / (FFT_SAMPLES))) * Input_Buffer[i];
//Hanning Window
//Input_Buffer_Window[i]=(0.5 * (1-cosf((2.0*PI*i) / (FFT_SAMPLES)))) * Input_Buffer[i];
//Flat top window
//Input_Buffer_Window[i]=(0.21557895 - 0.41663158 * cosf((2*PI*i) / (FFT_SAMPLES)) + 0.277263158 * cosf((4*PI*i) / (FFT_SAMPLES)) - 0.083578947 * cosf((6*PI*i) / (FFT_SAMPLES)) + 0.006947368 * cosf((8*PI*i) / (FFT_SAMPLES))) * Input_Buffer[i];
}*/
/*Bufor używany do obliczenia FFT, został stworzony, ponieważ funkcja FFT modyfikuje bufor wejściowy*/
for(uint16_t i=0; i<FFT_SAMPLES; i++)
{
Input_Buffer_FFT[i]=Input_Buffer[i];
/*Input_Buffer_FFT[i]=Input_Buffer_Window[i];*/
}
/*Funkcja obliczająca FFT*/
arm_rfft_fast_f32(&fft_handler,Input_Buffer_FFT,Output_Buffer_FFT, ifftFlag);
/*Funkcja obliczająca moduł z wartości rzeczywistej i urojonej dla każdego z prążków*/
arm_cmplx_mag_f32(Output_Buffer_FFT, Mag_Output_Buffer, fftSize/2);
/*Funkcja szukająca wartości maksymalnej*/
arm_max_f32(Mag_Output_Buffer, fftSize/2, &Max_Value_Mag_Buffer, &Max_Mag_Index);
/*Wydzielenie wartości rzeczywistej i urojonej z tablicy wyników FFT*/
for(uint16_t i=0; i<FFT_SAMPLES_HALF; i++)
{
real_Output_Buffer[i]=Output_Buffer_FFT[i*2];
imag_Output_Buffer[i]=Output_Buffer_FFT[(i*2)+1];
}
/*Tablica przesunięcia fazowego dla każdeo prążka*/
for(uint16_t i=0; i<FFT_SAMPLES_HALF; i++)
{
Angle_Output_Buffer[i]=atan2f(imag_Output_Buffer[i], real_Output_Buffer[i]);
}
/*Przesunięcie fazowe maksymalnego prążka*/
Angle_Max_Output_Buffer=atan2f(imag_Output_Buffer[Max_Mag_Index], real_Output_Buffer[Max_Mag_Index]);
/*Informacja o zakończeniu obliczeń*/
Calculation_finished=1;
/*Zerowanie wartości maksymalnej*/
Max_value=0;
}
}
Funkcja Callback informująca o zebraniu 512 próbek do bufora wejściowego. Zbieram dwa razy większą ilość próbek niż wykorzystywane do FFT, aby mieć pewność, że będzie wystarczająca ilość próbek.
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef* hadc)
{
if(hadc->Instance == ADC1)
{
if(Calculation_finished==1 || First_calculation_loop==1)
{
Calculation_finished=0;
Buffer_FFT_Status=1;
}
}
}
Sygnał z timera 2 informujący o częstotliwości próbkowania:
Częstotliwość próbkowania została ustawiona na 80 kHz poprzez wyzwalanie konwersji przetwornika ADC za pomocą timera 2:
Wyniki FFT:
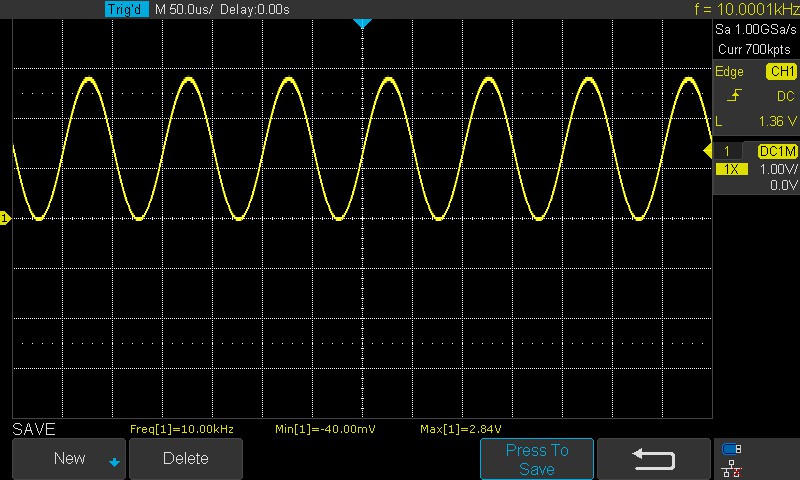
Przebieg z generatora funkcyjnego o częstotliwości 10kHz, na którym będzie wykonywane FFT:
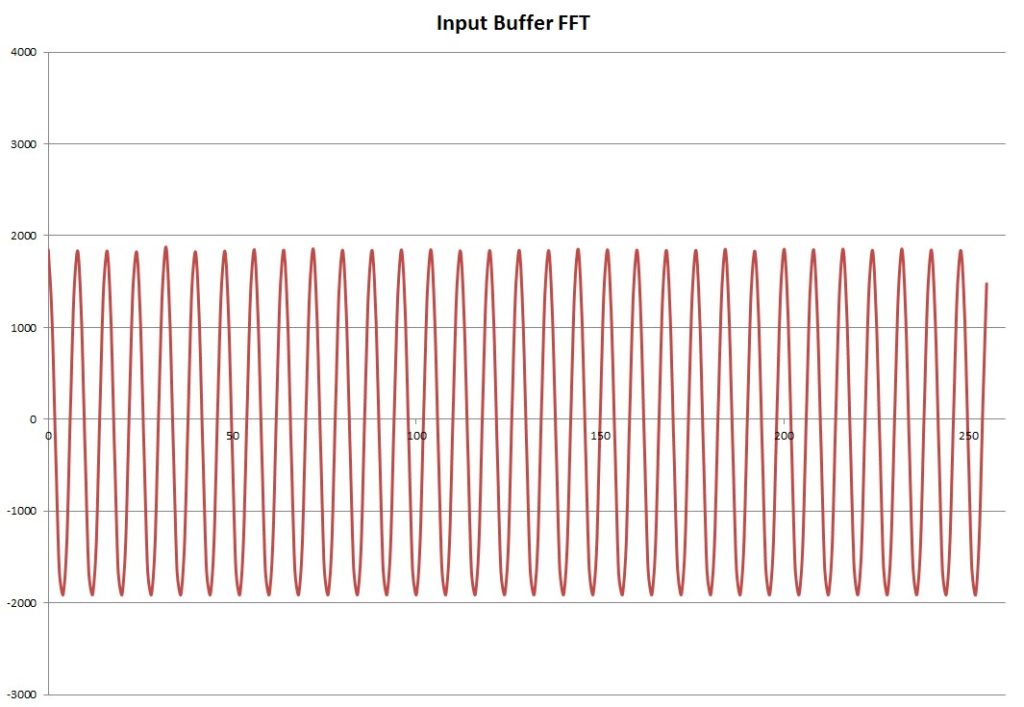
Bufor wejściowy do FFT jest to wycięty fragment przebiegu, oknem prostokątnym, składający się z 256 próbek, przesunięty o składową stałą w celu wyznaczenia największej energii z częstotliwości przebiegu. Próbki zostały odczytane za pomocą programu STMStudio.
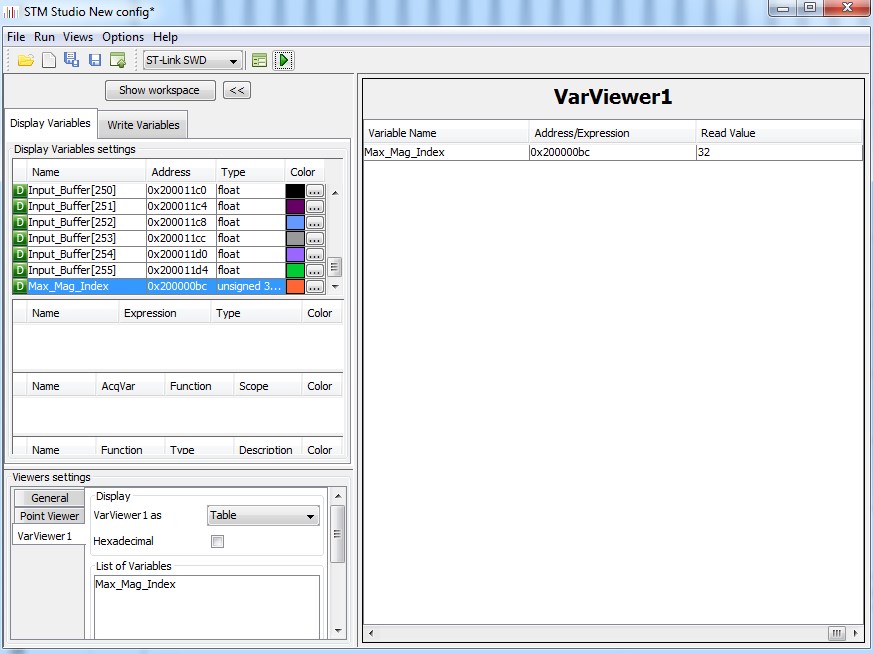
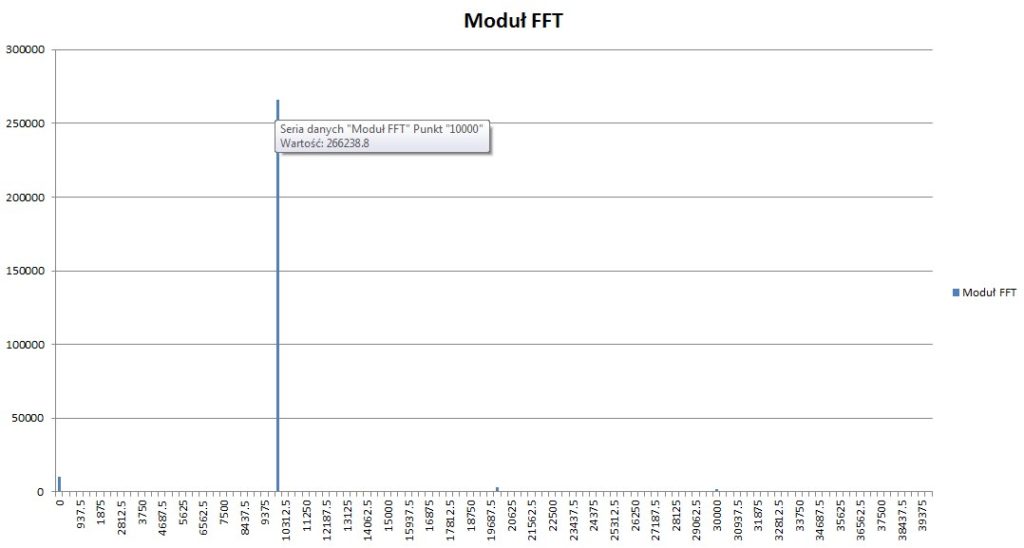
Po wykonaniu FFT na przebiegu o częstotliwości 10kHz, odczytano 32 prążek jako prążek o największej energii:
Wykorzystując okno prostokątne oraz 2^n okresów wyciek widma nie występuje, co można zaobserwować na Rys. 4. Podczas jednego okresu sinusoidy o częstotliwości 10kHz zbieranych jest 8 próbek, czyli w buforze składającym się z 256 próbek będzie 32 okresy.
Wyciek widma spowodowany złym doborem częstotliwości próbkowania:
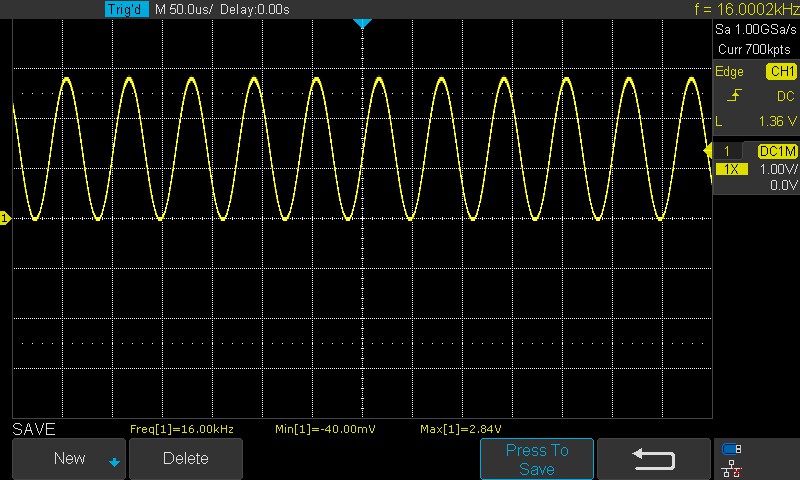
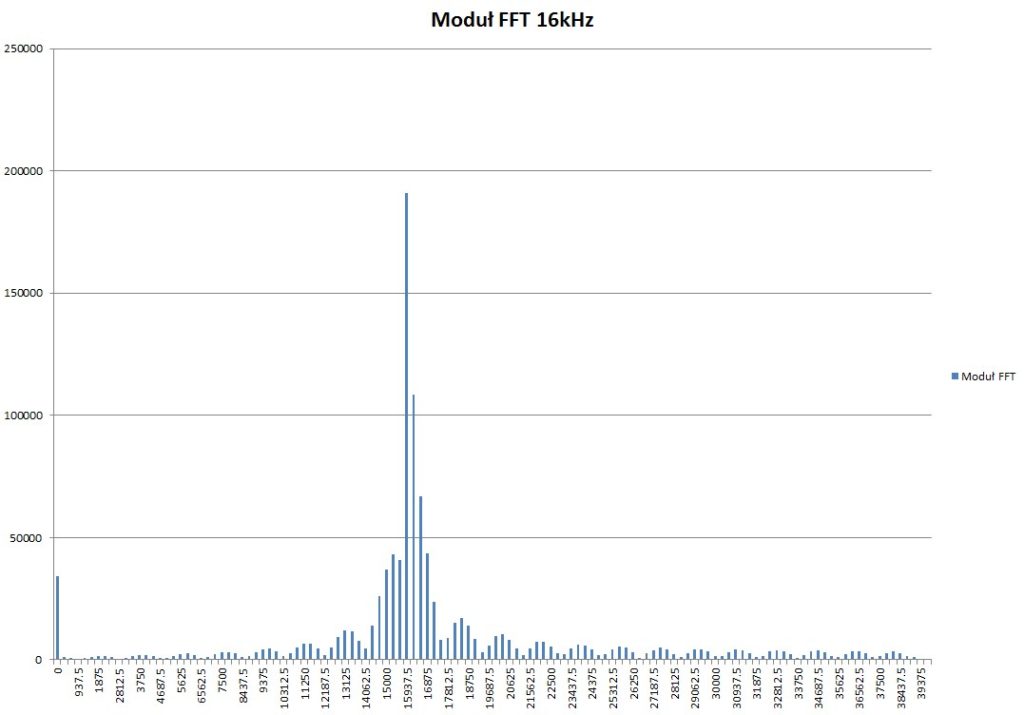
Następnie przy takich samych ustawieniach częstotliwości próbkowania przetwornika analogowo-cyfrowego, podałem sygnał sinusoidalny o częstotliwości 16kHz, czyli 5 okresów. Warunek o 2^n okresów nie został spełniony.
Niespełniony warunek o 2^n ilości okresów skutkuje tym, że pojawia się wyciek widma, co można zaobserwować na Rys. 7.
Wyciek widma spowodowany użyciem okien innych niż prostokątne, kiedy sygnał jest okresowy:
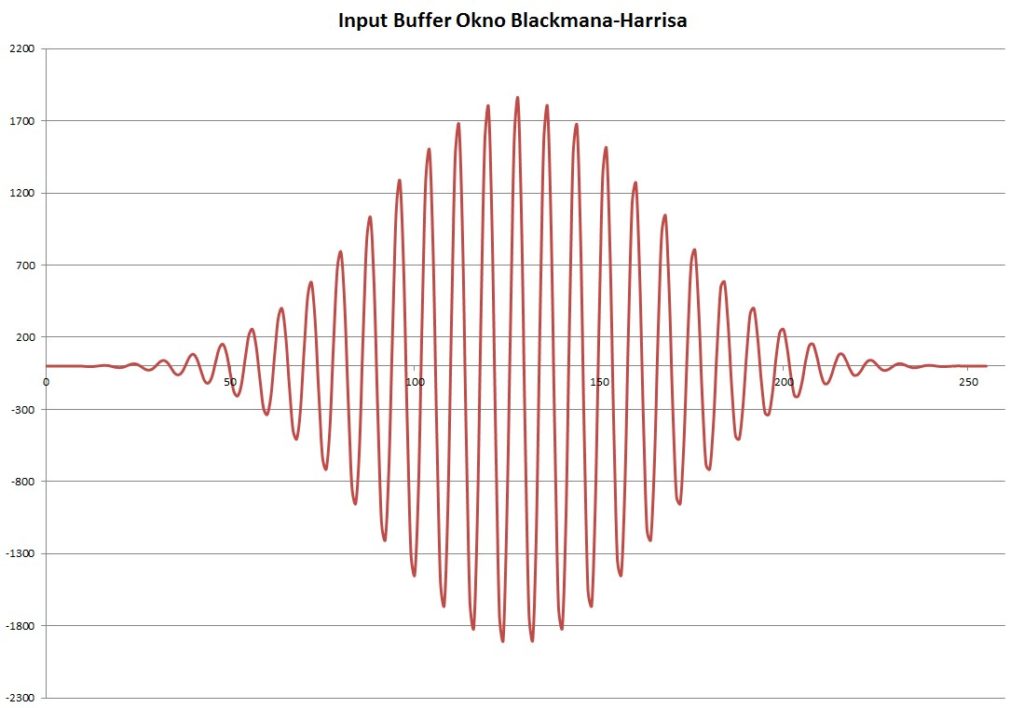
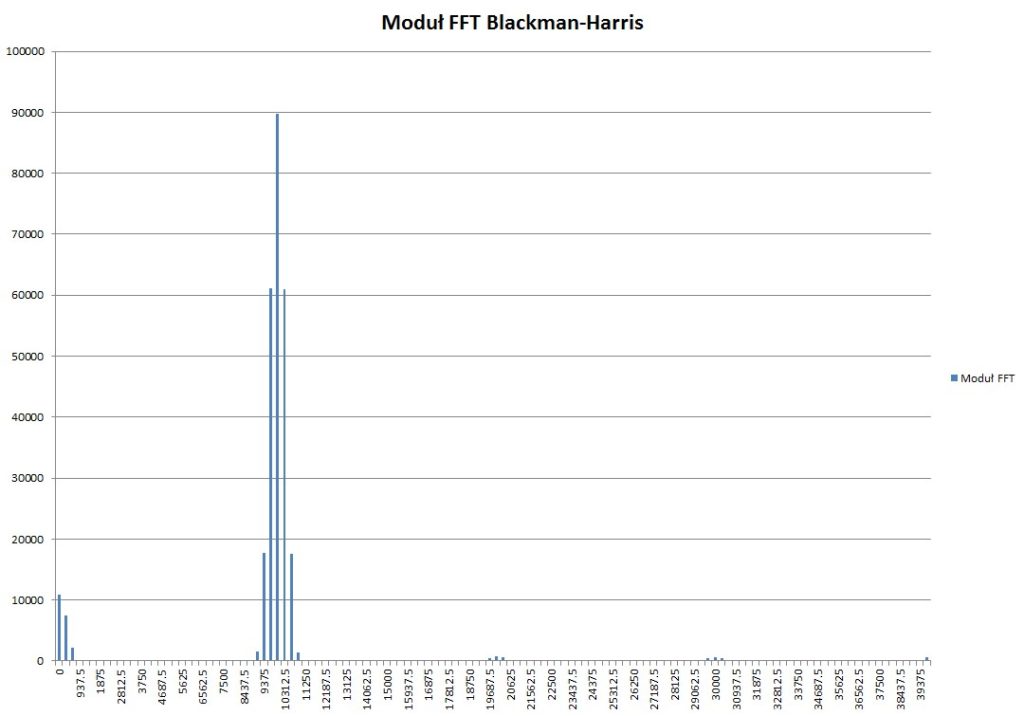
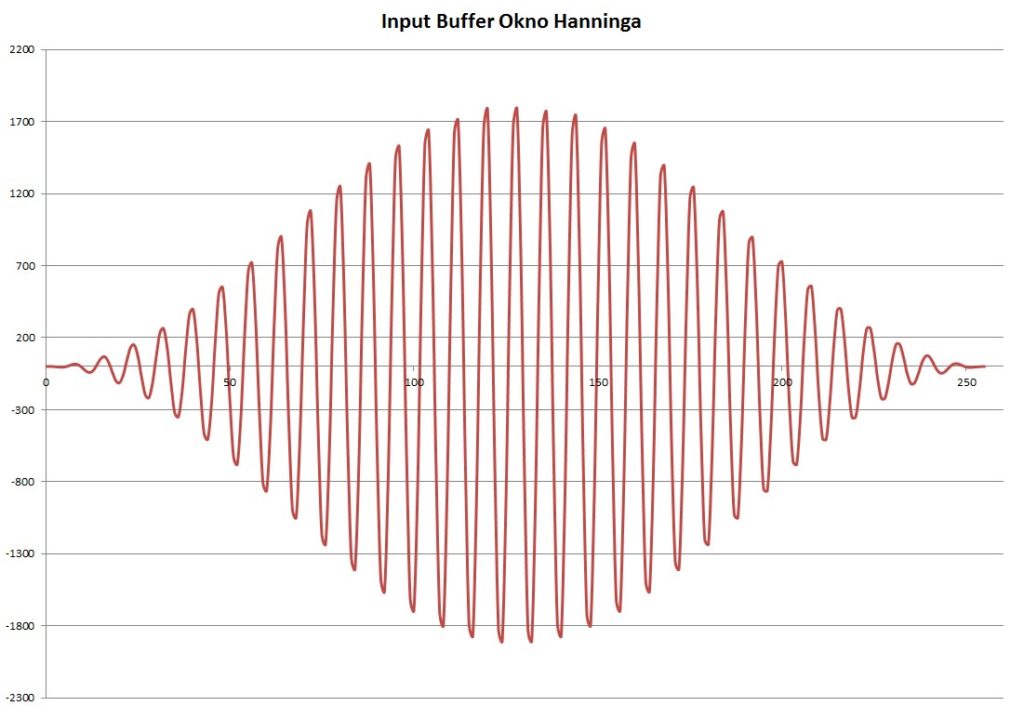
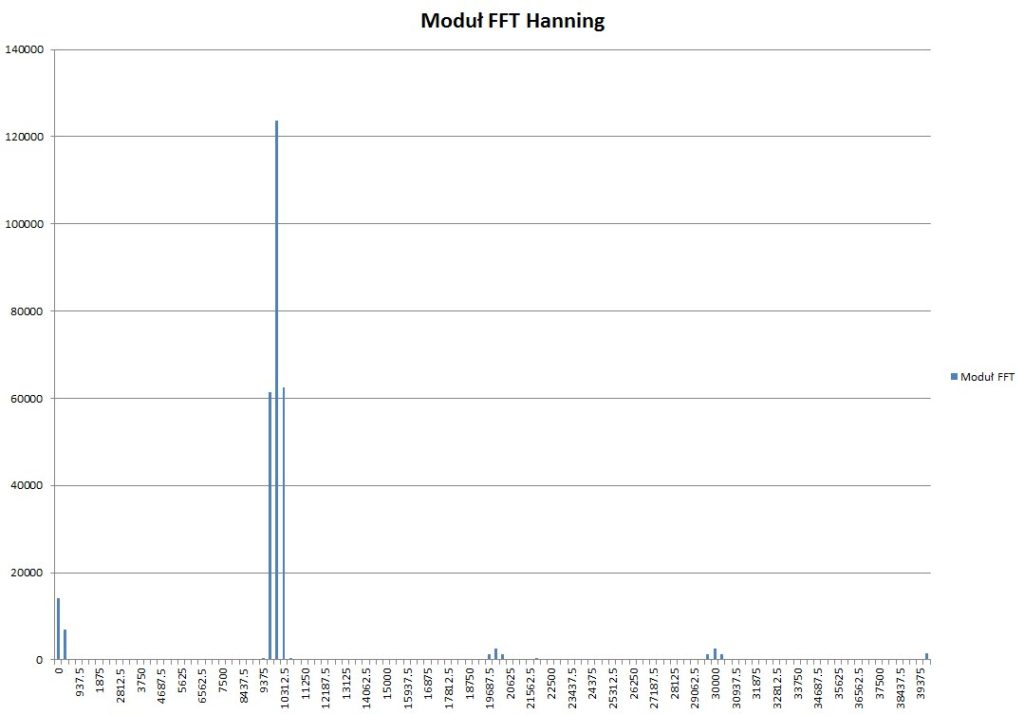
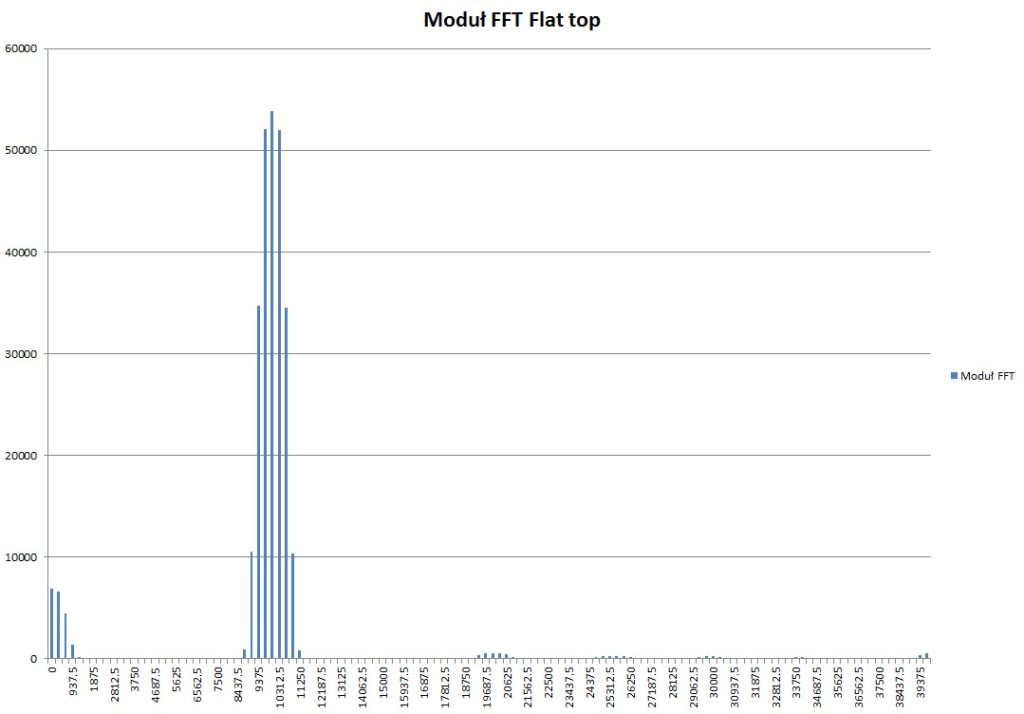
Okna są użyteczne, kiedy sygnał jest nieokresowy. Kiedy sygnał jest okresowy, najlepszym wyborem będzie okno prostokątne, co udowadniają poniższe wyniki dla różnych okien.
Obliczenia FFT z wykorzystaniem okien zostały wykonane na podstawie przebiegu z Rys. 2 (10kHz), przy tej samej częstotliwości próbkowania 80kHz.
Okno Blackmana-Harrisa:
Obliczone spektrum z przebiegu przemnożonego przez okno Blackmana-Harrisa:
Okno Hanninga:
Obliczone spektrum z przebiegu przemnożonego przez okno Hanninga:
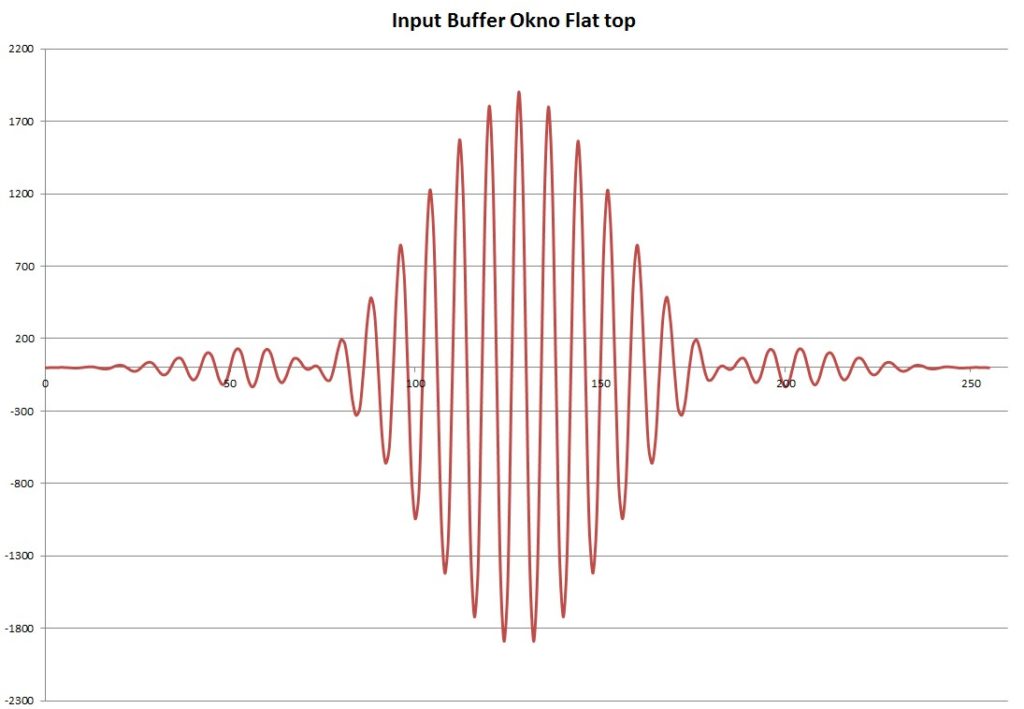
Okno flat top:
Obliczone spektrum z przebiegu przemnożonego przez okno Flat top:
Podsumowanie:
We wpisie zawarłem informację na temat programu służącego do wykonania FFT, przedstawiłem wyniki oraz omówiłem czynniki, które mają wpływ na wyciek widma.

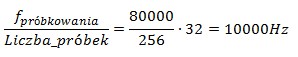
Super – wytłumaczone od podstaw (artykuł #1) . Dziękuję !
Spróbuję tą wiedzę wykorzystać w środowisku Arduino / ESP32 (bo ono jest mi lepiej znane) a może kiedyś znajdę ten artykuł w takiej wersji.
Generalnie wielkie dzięki za tak udostępnioną wiedzę !
Cieszę się bardzo, że podoba Ci się wpis, a tym bardziej że wykorzystasz go w praktyce.